MENCARI NILAI OPTIMUM MENGGUNAKAN UJI TITIK POJOK DAN METODE GARIS SELIDIK

MENCARI NILAI OPTIMUM MENGGUNAKAN UJI TITIK POJOK DAN METODE GARIS SELIDIK

Nilai Optimum Suatu Fungsi Objektif

·         Dalam pemodelan matematika masalah produksi ban PT. Samba Lababan, kalian akan mencari nilai x dan y sedemikian sehingga f (x, y) = 40.000x + 30.000y maksimum.

·         Bentuk umum dari fungsi tersebut adalah f (x, y) = ax + by. Suatu fungsi yang akan dioptimumkan (maksimum atau minimum). Fungsi ini disebut fungsi objektif.

·         Untuk menentukan nilai optimum fungsi objektif ini, kalian dapat menggunakan dua metode, yaitu :

1.      METODE UJI TITIK POJOK

Untuk menentukan nilai optimum fungsi objektif dengan menggunakan metode uji titik pojok, lakukanlah langkah-langkah berikut :

a.       Gambarlah daerah penyelesaian dari kendala-kendala dalam masalah program linear tersebut.

b.      Tentukan titik-titik pojok dari daerah penyelesaian itu.

c.       Substitusikan koordinat setiap titik pojok itu ke dalam fungsi objektif.

d.      Bandingkan nilai-nilai fungsi objektif tersebut. Nilai terbesar berarti menunjukkan nilai maksimum dari fungsi f(x, y), sedangkan nilai terkecil berarti menunjukkan nilai minimum dari fungsi f(x, y)

Contoh I :

Sebagai contoh, kalian akan memaksimumkan keuntungan PT. Samba Lababan dari produksi ban dengan model matematika f(x, y) = 40.000x +  30.000y.

 

Perhatikan daerah penyelesaian dari grafik pada gambar di atas.

o    Titik-titik pojoknya adalah titik O, A, B, C, dan D.

o    Titik O adalah titik pusat koordinat. Jadi, titik O(0,0).

o    Titik A adalah titik potong antara garis x = 80 dan sumbu-x

Jadi, titik A(80, 0).

o    Titik B adalah titik potong antara garis x = 80 dan garis

8x + 4y = 800.
Substitusi x = 80 ke persamaan 8x + 4y = 800
 8 . 80 + 4y = 800
               y = 40
Jadi, titik B(80, 40).

o    Titik C adalah titik potong antara garis 8x + 4y = 800 dan

2x + 5y = 800.
Dari 8x + 4y = 800 didapat y = 200 - 2x.
Substitusi nilai y ke persamaan 2x + 5y = 800
      2x + 5(200 - 2x) = 800
      2x + 1000 - 10x = 800
                        - 8x = - 200
                            x = 25
Substitusi x = 25 ke persamaan y = 200 - 2x
      y = 200 - 2 · 25
     y = 150
Jadi, titik C(25, 150).

o    Titik D adalah titik potong antara garis 2x + 5y = 800 dan sumbu-y.

Substitusi x = 0 ke persamaan 2x + 5y = 800
   2 . 0 + 5y = 800
              5y = 800
                y = 160
Jadi, titik D(0, 160).

o    Uji titik-titik pojok ke fungsi objektif f(x, y) = 40.000x + 30.000y, sehingga fungsi objektif ini maksimum.

Titik Pojok (x, y)	f(x, y) = 40.000x + 30.000y
A (80, 0)	3.200.000
B (80, 40)	4.400.000
C (25, 150)	5.500.000
D (0, 160)	4.800.000

Dari tabel tersebut dapat diperoleh nilai maksimum fungsi objektif f(x, y) = 40.000x + 30.000y adalah f(25, 150) = 5.500.000. Jadi, PT. Samba Lababan harus memproduksi 25 ban motor dan 150 ban sepeda untuk memperoleh keuntungan maksimum.

Untuk menentukan nilai minimum dilakukan langkah yang sama. Lebih jelasnya, perhatikan contoh berikut ini.

·         Contoh II :

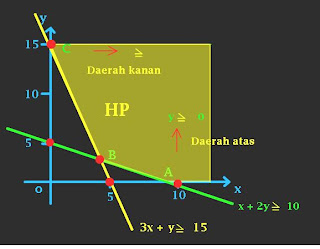
Tentukan nilai minimum fungsi objektif f(x, y) = 2x + 10y yang memenuhi x + 2y ≥ 10, 3x +  y ≥ 15, x ≥ 0, dan y ≥ 0.

Titik-titik pojoknya adalah titik A, B, dan C.

• Titik A adalah titik potong garis x + 2y = 10 dengan sumbu-x.

   Substitusi y = 0 ke persamaan x + 2y = 10.
         x + 2y = 10

x + 2 . 0 = 10
           x = 10
Jadi, titik A(0, 10).

• Titik B adalah titik potong garis x + 2y =10 dengan garis 3x +  y = 15

Dari x + 2y = 10 diperoleh x = 10 - 2y.
Substitusi nilai x ke persamaan 3x +  y = 15
               3x + y = 15
   3(10 - 2y) + y = 15
       30 - 6y + y = 15

   - 5y = 15

                5y = 30 - 15
                 5y = 15 ↔ y = 3

Substitusi nilai y = 3 ke persamaan x = 10 - 2y
x = 10 􀀐 2y
  = 10 – 2 . 3
  = 10 - 6
  =  4
Jadi, titik B(4, 3).

• Titik C adalah titik potong garis 3x + y = 15 dengan sumbu-y.

Substitusi x 􀀠 0 ke persamaan 3x + y = 15.
   3x + y = 15
3 . 0 + y = 15
           y = 15
Jadi, titik C(0, 15).

• Uji titik-titik pojok

Titik Pojok (x, y)	f(x, y) = 2x + 10y
A (10, 0)	20
B (4, 3)	38
C (0, 15)	150

Dari tabel diperoleh nilai minimum fungsi objektif f(x, y) = 2x + 10y adalah f(10, 0) = 20.

2.      METODE GARIS SELIDIK

Untuk menentukan nilai optimum fungsi objektif dengan menggunakan metode garis selidik, lakukanlah langkah-langkah berikut :

·         Tentukan garis selidik, yaitu garis-garis yang sejajar dengan garis ax + by = k, a > 0, b > 0, dan k Є R.

·         Gambarkan garis selidik-garis selidik tersebut pada koordinat Cartesius!

·         Untuk menentukan nilai maksimum fungsi tujuan maka carilah garis selidik yang jaraknya terbesar terhadap titik pusat O(0, 0) dan berada pada daerah penyelesaian. Sedangkan untuk menentukan nilai minimum fungsi tujuan maka carilah garis selidik yang jaraknya terkecil terhadap titik pusat O(0, 0) dan berada pada daerah penyelesaian

Contoh :

Grafik berikut ini adalah produksi ban PT. Samba Lababan

( Daerah Penyelesaian memenuhi x + 2y ≥ 10, 3x +  y ≥ 15, x ≥ 0, dan y ≥ 0 )

Garis selidik dari fungsi objektif f(x, y) = 40.000x + 30.000y adalah
 4x + 3y = k.

Ambil k = 120, didapat garis selidik 4x + 3y = 120.
Ambil k = 240, didapat garis selidik 4x + 3y = 240.
Ambil k = 550, didapat garis selidik 4x + 3y = 550.

Gambarkan garis-garis selidik ini sehingga kamu dapat menentukan nilai maksimum fungsi objektif f(x, y) = 40.000x + 30.000y.

Perhatikan bahwa garis selidik yang menyebabkan fungsi objektif maksimum adalah 4x + 3y = 550.

Dengan mengalikan kedua ruas persamaan garis selidik dengan 10.000, kamu mendapatkan nilai maksimum fungsi objektif sebagai berikut :

           10.000(4x + 3y) = 10.000(550)

       40.000x + 30.000y = 5.500.000

Jadi, nilai maksimum fungsi objektif f(x, y) = 40.000x + 30.000y adalah 5.500.000.

Dari gambar di atas tampak bahwa garis selidik 4x + 3y = 550 melalui titik

C(25, 150). Ini berarti, fungsi objektif f(x, y) = 40.000x + 30.000y
mencapai maksimum pada titik C(25, 150).

Jadi, PT. Samba Lababan harus memproduksi 25 ban motor dan 150 ban sepeda untuk memperoleh keuntungan maksimum Rp5.500.000,00.